使用Matlab的Appdesigner设计GUI界面,显示弹道曲线
使用龙格库塔法(定步长四阶)解算弹道方程
概略
最近在完成课程大作业的过程中接触到了GUI界面的制作,大作业主要是使用龙格库塔法(定步长四阶)解算弹道方程,并通过GUI将弹道曲线显示出来。开始着手设计GUI的时候,查找资料大多是关于GUIDE的,直到有一天在官网上看到了Appdesigner,发现要友好易用很多,转而使用Appdesigner。
龙格库塔法
龙格库塔法是一类数值解微分方程的算法, 其中较常见的是四阶龙格库塔法。公式如下:
下一个值(yn+1)由现在的值(yn)加上时间间隔(h)和一个估算的斜率的乘积所决定。该斜率是以下斜率的加权平均:
- 是时间段开始时的斜率;
- 是时间段中点的斜率,通过欧拉法采用斜率来决定在点的值;
- 也是中点的斜率,但是这次采用斜率决定值;
- 是时间段终点的斜率,其值用决定。
GUI设计流程
首先在命令中输入appdesigner进入设计界面,App designer支持的控件很多,首先拖选编辑控件,完成设计UI界面。
可用控件列表如下:
根据需要设计的GUI,包括一个坐标图显示,落点坐标显示,以及多个参数输入,UI的设计和代码实现是相对独立的,可以先进行UI的排版布局:
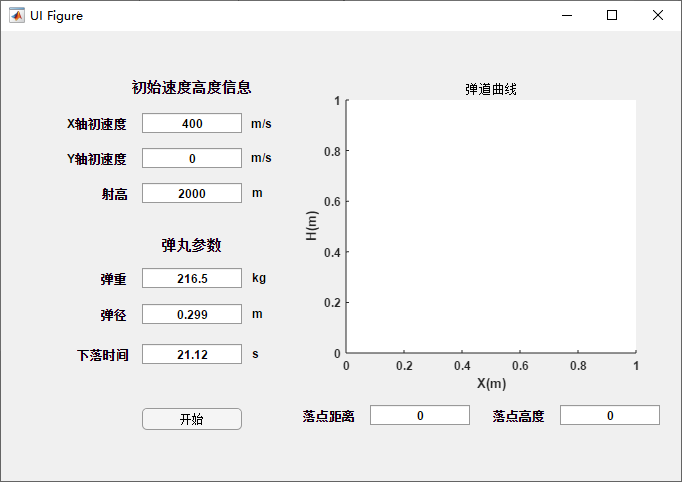
控件可以设置默认值,作为输入参数使用。UI设计完成后需要进行解算函数和计算控制函数的编写。
添加按钮触发回调函数,在代码视图中,可通过代码浏览器添加回调。这里我在按下开始按钮后对变量进行赋值,并调用calculate函数进行计算:
% Button button pushed function
function ButtonButtonPushed_start(app)
global u0; global w0; global H; %变量初始化
global q;global d;global tf;
u0=app.NumericEditField.Value; %x轴方向初速度
w0=app.NumericEditField2.Value; %y轴方向初速度
H=app.NumericEditField4.Value; %射高
q=app.NumericEditField3.Value; %弹丸重量
d=app.NumericEditField7.Value; %弹丸直径
tf=app.NumericEditField9.Value; %下落时间
calcaulate(app); %调用计算函数
end
然后根据龙格库塔法编写calculate函数:
methods (Access = private)
function results = calcaulate(app)
format long
global C;global G;global H;global ton;global R;
global u0; global w0;
global q;global d;global tf;
%气象条件
hon=760;ton=288.4*1000;R=29.27;G=5.862/1000;eon=8.4;Cxo=0.160;
%相关参数计算
C=Cxo/0.65*d*d/q*1000;
h=0.01;tatal=tf/h;%初始化循环计算次数
x3=H;x4=0;t=0;
p0=w0/(u0^2+w0^2)^0.5;%计算速度比
x=[u0,p0,H,0];
for i=1:tatal %四阶龙格库塔
k1=h*dif_equation_group(app,t,x);
k2=h*dif_equation_group(app,t+h/2,x+0.5*k1);
k3=h*dif_equation_group(app,t+h/2,x+0.5*k2);
k4=h*dif_equation_group(app,t+h,x+k3);
x=x+(k1+2*k2+2*k3+k4)/6;
dx=dif_equation_group(app,t+h,x);
x3=[x3;x(3)];
x4=[x4;x(4)];
t=t+h;
end
plot(app.UIAxes,x4,x3,'-r'); %在GUI中画出弹道曲线
app.NumericEditField6.Value=x(4); %显示落点数据
app.NumericEditField8.Value=x(3);
end
end
methods (Access = private)
function dx = dif_equation_group(app,t,x)
global C;global G;global H;global ton;global R;
Ma=(1+x(2)^2)^0.5*x(1)/20.074*(300.124-0.005862*x(3))^0.5;
if Ma<0.8 CxoM=0.6;
else if (0.8<Ma)&&(Ma<1.2) CxoM=Ma-0.1;
else CxoM=1.1;
end
end
dx(1)=-4.737e-4*C*( 1-G/ton*( H-x(3)) )^(1/(R*G))*ton/( ton+G*(2000-x(3)) )*CxoM*(1+x(2)^2)^0.5*x(1)^2;
dx(2)=-9.806/x(1);
dx(3)=x(1)*x(2);
dx(4)=x(1);
end
end
运行结果
初始参数弹道: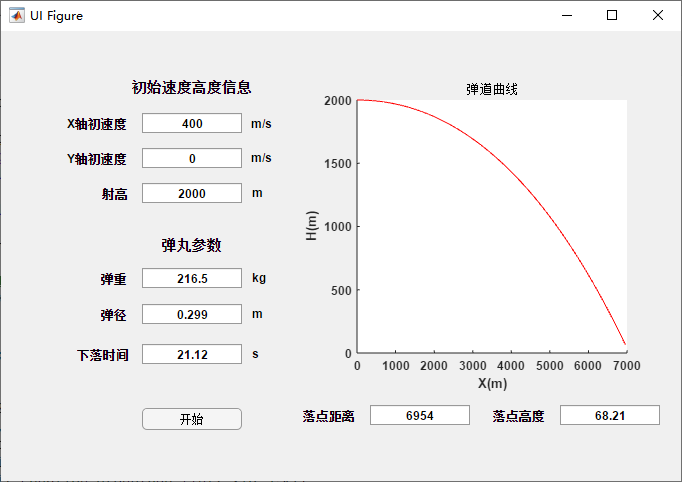
改变y轴初速度: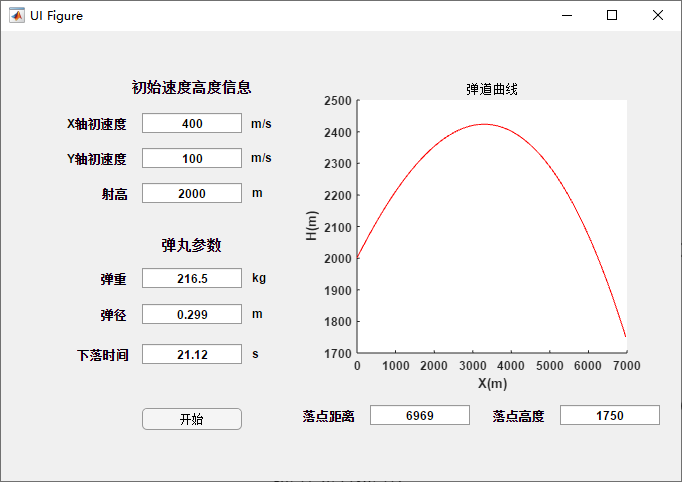
最后尝试导出exe可执行文件,但是不成功,只能导出matlab可执行文件,所以不能脱离matlab运行。
本网站文章版权均为本人所有,未经同意不得私自搬运复制,欢迎注明引用出处的合理转载,图片转载请留言。文章内容仅用于技术研究和探索,不得用于违法目的。