FPGA秋招学习笔记整理（1）

2021-09-26 · 9 min read

FPGA autumn recruit study notes (one) : Fundamentals of Digital Circuits
FPGA秋招学习笔记整理(1)：数电基础知识

常用进制

进制	符号	进位基数
二进制	B	2
八进制	O	8
十进制	D	10
十六进制	H	16

进制的转换

各进制与十进制的转换
将其各位按权重展开相加，即可得到十进制数。例如:

10110_2=1\times2^4+0\times2^3+1\times2^2+0\times2^0=22_{10}

十进制转换为其他进制
整数部分使用基数除法进行计算，将要转换的数除以新的进制的基数，把余数作为新进制的的最低位，再把上一次的商除以新的进制基数，把余数作为新进制的次低位，直到最后的商为零，这时余数就是新进制的最高位。
小数部分使用基数乘法进行计算，将要转换的数乘以新的进制的基数，把得到的整数部分作为新进制小数部分的最高位，再把上一次的小数部分乘以新的进制基数，把整数部分作为新进制的次低位，直到小数部分变为0；

数的原码，补码，反码

三种表示方法均有符号位和数值位两部分，符号位都是用0表示“正”，用1表示“负”，而数值位，三种表示方法各不相同。

原码：是最简单的机器数表示法，用最高位表示符号位，其他位存放该数的二进制的绝对值。
以带符号位的四位二进制数为例：1010，最高位为1表示这是一个负数，其它三位010，即 $0*2^2+1*2^1+0*2^0=2$ ，所以1010表示十进制数-2。
反码：正数的反码还是等于原码；负数的反码就是它的原码除符号位外，按位取反。
以带符号位的四位二进制数为例：3是正数，反码与原码相同，则可以表示为0011；-3的原码是1011，符号位保持不变，低三位按位取反，所以-3的反码为1100。
补码：正数的补码等于它的原码；负数的补码等于反码+1.补码系统的最大优点是可以在加法或减法处理中，不需因为数字的正负而使用不同的计算方式。只要一种加法电路就可以处理各种有符号数加法，而且减法可以用一个数加上另一个数的补码来表示，因此只要有加法电路和补码电路即可以完成各种有符号数加法和减法，方便电路设计。

例子：

十进制	原码	反码	补码
6	0000 0110	0000 0110	0000 0110
-3	0000 0110	1111 1100	1111 1101

  6 - 3 ==> 6 + (-3)
  0000 0110 // 6(补码)
+ 1111 1101 // -3(补码)
----------------------
  0000 0011 // 3(补码)

逻辑门

逻辑门是在集成电路上的基本组件。简单的逻辑门可由晶体管组成。这些晶体管的组合可以使代表两种信号的高低电平在通过它们之后产生高电平或者低电平的信号。高、低电平可以分别代表逻辑上的“真”与“假”或二进制当中的1和0，从而实现逻辑运算。

类型	名称	逻辑函数	真值规则
AND	与门	$A\cdot B$	有0输出0
OR	或门	$A+B$	有1输出1
NOT	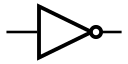非门	$\overline A$	输出反向
NAND	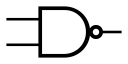与非门	$\overline {A\cdot B}$	同1输出1
NOR	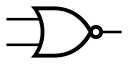或非门	$\overline {A+B}$	同0输出1
XOR	异或门	$A\oplus B$	相异输出1

逻辑代数计算

参与逻辑运算的变量叫逻辑变量，用字母A，B……表示。每个变量的取值非0 即1。 0、1不表示数的大小，而是代表两种不同的逻辑状态。

正、负逻辑规定：

正逻辑体制规定：高电平为逻辑1，低电平为逻辑0。
负逻辑体制规定：低电平为逻辑1，高电平为逻辑0。

逻辑函数：如果有若干个逻辑变量（如A、B、C、D）按与、或、非三种基本运算组合在一起，得到一个表达式L。对逻辑变量的任意一组取值（如0000、0001、0010）L有唯一的值与之对应，则称L为逻辑函数。逻辑变量A、B、C、D的逻辑函数记为： $L=f(A、B、C、D)$

逻辑函数的标准形式

逻辑变量的逻辑与运算叫做与项，与项的逻辑或运算构成了逻辑函数的与或式。
逻辑变量的逻辑或运算叫做或项，或项的逻辑与运算构成了逻辑函数的或与式。
最小项
对于 n 个变量的逻辑函数而言，它的与项如果包含全部 n 个变量，即每个变量以原变量或反变量的形式出现一次且只出现一次，那么这个与项就称为该逻辑函数的最小项。
最大项
对于 n 个变量的逻辑函数而言，它的或项如果包含全部n 个变量，即每个变量以原变量或反变量的形式出现一次且只出现一次，那么这个或项就称为该逻辑函数的最大项。

最大项和最小项的性质：
n变量的全部最小项之和恒为1，全部最大项之积恒为0.
任意两个最小项之积恒为0,任意两个最大项之和恒为1.
n变量的每一个最小项或者最大项有n个相邻项（相邻项是指两个最小项只有一个因子互为反变量，其余因子均相同，又称逻辑相邻项）

化简公式

定律名称	或式	与式
0-1律	$1+A=1,0+A=A$	$1 \cdot A=A,0\cdot A=0$
重叠律	$A+A=A$	$A\cdot A=A$
互补律	$A+\overline A=1$	$A\cdot \overline A=0$
还原律	$\overline{\overline A}=A$	$\overline{\overline A}=A$
交换律	$A+B=B+A$	$A\cdot B=B\cdot A$
结合律	$A+(B+C)=(A+B)+C$	$A\cdot (B\cdot C)=(A\cdot B)\cdot C$
分配率	$A+B\cdot C = (A+B)\cdot (A+C)$	$A\cdot (B+C) = (A\cdot B)(A\cdot B)$
反演律	$\overline {A+B} = \overline A\cdot \overline B$	$\overline{A\cdot B} = \overline A + \overline B$
吸收律	$A+A\cdot B=A,A\cdot B+A\cdot \overline B=A,A+\overline A \cdot B=A+B$	$A\cdot (A+B)=A,(A+B)(A+\overline B)=A,A(\overline A+B)=AB$
冗余律	$AB+\overline AC+BC=AB+\overline AC$	$(A+B)(\overline A+C)(B+C)=(A+B)(\overline A +C)$

逻辑函数的卡诺图化简

将函数化为最小项之和的形式，然后做函数的卡诺图，确定卡诺图方格矩阵
画卡诺圈（要遵循卡洛圈最少，最大的原则）
写逻辑表达式（相同变量留下，不同变量去掉）

https://segmentfault.com/a/1190000021511009
https://zhuanlan.zhihu.com/p/99082236
https://zh.wikipedia.org/wiki/%E9%82%8F%E8%BC%AF%E9%96%98
https://blog.csdn.net/vivid117/article/details/100547649

若需要md版本或者pdf版本，请邮件联系邮箱。

本网站文章版权均为本人所有，未经同意不得私自搬运复制，欢迎注明引用出处的合理转载，图片转载请留言。文章内容仅用于技术研究和探索，不得用于违法目的。

📋阅读量: 0